Soal 1
Bentuk sederhana dari aljabar adalah . . . .
adalah . . . .
A.)
B.)
C.
D.
Pembahasan:
Satu hal yang perlu kalian ingat ketika kita akan menjumlahkan atau mengurangkan suku - suku aljabar, kita harus ingat aturan kaidah sejenis, dimana suku aljabar yang bisa dijumlahkan atau dikurangkan hanyalah yang memiliki variabel sejenis.
Pada bentuk aljabar soal diatas yang merupakan suku sejenis adalah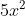 dan
dan  ,
,  dan
dan  , - 8xy dan 12xy. Suku suku itulah yang bisa kita jumlahkan
, - 8xy dan 12xy. Suku suku itulah yang bisa kita jumlahkan
Coba perhatikan ya . . .



Karena ketiga suku mengandung angka 4, kita bisa juga ubah dengan mengeluarkan angka 4 nya, sehingga bentuknya jadi seperti ini :
)
Jadi jawabannya adalah yang C
Soal 2
Hasil penjumlahan 10x - 5y - 6z dan - 5x + 2y + 4z adalah . . . .
A. 15x - 7y - 10z
B. -5x -3y + 2z
C. 5x - 3y -2z
D. 5x + 7y + 10z
Pembahasan
Untuk menjumlahkan dua bentuk aljabar diatas jangan lupa iberi kurung masing masingnya, karena kita akan mengalikan tanda penjumlahan atau tanda pengurangan ke dalam bentuk aljabar kedua. Agar lebih paham coba perhatikan caranya ya....
= (10x - 5y - 6z) + (- 5x + 2y + 4z)
= 10x - 5y - 6z - 5x + 2y + 4z
Kemudian kelompokkan suku - suku yang sejenis
= 10x - 5x - 5y + 2y - 6z + 4z
= 5x - 3y - 2z
Jadi jawabannnya adalah C
Soal 3
Hasil pengurangan - 7a + 4b - 2c oleh - 5a + 3b - 5c adalah . . . .
A. 2a - b + 3c
B. - 2a + b + 3c
C. - 2a + 7b - 3c
D. 2a + b - 3c
Pembahasan
Bentuk lain dari soal pengurangan aljabar adalah adanya kata kata pengurangan "oleh" atau pengurangan "dari". Jika kata "oleh" artinya bentuk aljabar pertama di kurangkan oleh aljabar kedua, tetapi jika ada kata "dari" maka sebaliknya, bentuk aljabar kedua yang dikurangi aljabar pertama.
Soal diatas mengandung kata "pengurangan oleh" sehingga yang dikurangkan adalah bentuk aljabar pertama oleh kedua.
= (- 7a + 4b - 2c) - (- 5a + 3b - 5c)
Terdapat pengalian tanda - dengan semua tanda pada suku aljabar kedua
= - 7a + 4b - 2c + 5a - 3b + 5c
= -7a + 5a + 4b - 3b - 2c + 5c
= - 2a + b + 3c
Jadi jawabannya adalah B
Soal 4
Jika - 2x + 3y dikurangkan dari 2x + 3y, maka hasilnya adalah . . . .
A. 6y
B. - 6y
C. 4x
D. - 4x
Jadi jawabannya adalah C
Pembahasan
Soal diatas terdapat kata " dikurangkan dari" maka yang kita lakukan adalah pengurangan bentuk aljabar kedua dengan yang pertama.
= (2x + 3y) - ( - 2x + 3y)
= 2x + 3y + 2x - 3y
= 2x + 2x +3y - 3y
= 4x
Soal 5
Hasil pengurangan - 2(x + 4) dari -6(x - 2) adalah . . . .
A. - 4x + 20
B. 6x - 20
C. - 8x + 4
D. 4x - 20
Pembahasan
Soal ini sama dengan diatas, jadi yang dikurangkan adalah bentuk aljabar kedua dikurangi yang pertama. Perbedaannya adalah terdapat pengalian bilangan dengan suku aljabar. Jadi langkah pertama yang akan kita lakukan adalah mengalikan angka itu dengan masing masing suku aljabarnya.
= - 2 ( x + 4) = (- 2 . x ) + ( - 2 . 4) = -2x - 8
= - 6 ( x - 2) = ( - 6. x) - (- 6 . 2) = - 6x + 12
Jadi yang akan dikurangkan adalah - 6x + 12 oleh -2x - 8
= (- 6x + 12) - (-2x - 8)
= - 6x + 12 + 2x + 8
= - 6x + 2x + 12 + 8
= - 4x + 20
So, jawabannya adalah A
Soal 6
Penyederhanan dari adalah . . . .
adalah . . . .
A.
B.
C.
D.
Pembahasan
Bagaimana jika yang dijumlahkan aljabarnya dalam bentuk pecahan??? Tenang saja, ini cukup mudah kok. Kalian hanya perlu mengingat kaidah penjumlahan dan pengurangan pada pecahan biasa.
\pm&space;(bxc)}{bxd})
Pada soal diatas yang menjadi :
a = 5
b = x + 1
c = 6
d = x + 4
Setelah itu, tinggal kita ikuti seperti rumus di atas
=)&space;-&space;6(x+1)}{(x+1)(x+4)})
Yang diatas tinggal kita kalikan angkanya ke dalam suku aljabar, sedangkan yang dibawah kita kalikan menggunakan aturan pengalian suku dua aljabar. Kalian pasti sudah tau caranya.....
=-(6x+6)}{x^{2}&space;+5x+&space;4})
Kemudian buka kurung yang diatas dan selesaikan oerasinya
=
=
Jadi jawabannya adalah B
Sekian dulu postingan kali ini, semoga dapat mebantu kalian dalam belajar ataupun proses pembelajaran. Jangan lupa di share ya artikel ini.....dan kunjungi juga artikel artikel menarik lainnya. Terimakasih . . . .
Bentuk sederhana dari aljabar
A.
B.
C.
D.
Pembahasan:
Satu hal yang perlu kalian ingat ketika kita akan menjumlahkan atau mengurangkan suku - suku aljabar, kita harus ingat aturan kaidah sejenis, dimana suku aljabar yang bisa dijumlahkan atau dikurangkan hanyalah yang memiliki variabel sejenis.
Pada bentuk aljabar soal diatas yang merupakan suku sejenis adalah
Coba perhatikan ya . . .
Karena ketiga suku mengandung angka 4, kita bisa juga ubah dengan mengeluarkan angka 4 nya, sehingga bentuknya jadi seperti ini :
Jadi jawabannya adalah yang C
Soal 2
Hasil penjumlahan 10x - 5y - 6z dan - 5x + 2y + 4z adalah . . . .
A. 15x - 7y - 10z
B. -5x -3y + 2z
C. 5x - 3y -2z
D. 5x + 7y + 10z
Pembahasan
Untuk menjumlahkan dua bentuk aljabar diatas jangan lupa iberi kurung masing masingnya, karena kita akan mengalikan tanda penjumlahan atau tanda pengurangan ke dalam bentuk aljabar kedua. Agar lebih paham coba perhatikan caranya ya....
= (10x - 5y - 6z) + (- 5x + 2y + 4z)
= 10x - 5y - 6z - 5x + 2y + 4z
Kemudian kelompokkan suku - suku yang sejenis
= 10x - 5x - 5y + 2y - 6z + 4z
= 5x - 3y - 2z
Jadi jawabannnya adalah C
Soal 3
Hasil pengurangan - 7a + 4b - 2c oleh - 5a + 3b - 5c adalah . . . .
A. 2a - b + 3c
B. - 2a + b + 3c
C. - 2a + 7b - 3c
D. 2a + b - 3c
Pembahasan
Bentuk lain dari soal pengurangan aljabar adalah adanya kata kata pengurangan "oleh" atau pengurangan "dari". Jika kata "oleh" artinya bentuk aljabar pertama di kurangkan oleh aljabar kedua, tetapi jika ada kata "dari" maka sebaliknya, bentuk aljabar kedua yang dikurangi aljabar pertama.
Soal diatas mengandung kata "pengurangan oleh" sehingga yang dikurangkan adalah bentuk aljabar pertama oleh kedua.
= (- 7a + 4b - 2c) - (- 5a + 3b - 5c)
Terdapat pengalian tanda - dengan semua tanda pada suku aljabar kedua
= - 7a + 4b - 2c + 5a - 3b + 5c
= -7a + 5a + 4b - 3b - 2c + 5c
= - 2a + b + 3c
Jadi jawabannya adalah B
Soal 4
Jika - 2x + 3y dikurangkan dari 2x + 3y, maka hasilnya adalah . . . .
A. 6y
B. - 6y
C. 4x
D. - 4x
Jadi jawabannya adalah C
Pembahasan
Soal diatas terdapat kata " dikurangkan dari" maka yang kita lakukan adalah pengurangan bentuk aljabar kedua dengan yang pertama.
= (2x + 3y) - ( - 2x + 3y)
= 2x + 3y + 2x - 3y
= 2x + 2x +
= 4x
Soal 5
Hasil pengurangan - 2(x + 4) dari -6(x - 2) adalah . . . .
A. - 4x + 20
B. 6x - 20
C. - 8x + 4
D. 4x - 20
Pembahasan
Soal ini sama dengan diatas, jadi yang dikurangkan adalah bentuk aljabar kedua dikurangi yang pertama. Perbedaannya adalah terdapat pengalian bilangan dengan suku aljabar. Jadi langkah pertama yang akan kita lakukan adalah mengalikan angka itu dengan masing masing suku aljabarnya.
= - 2 ( x + 4) = (- 2 . x ) + ( - 2 . 4) = -2x - 8
= - 6 ( x - 2) = ( - 6. x) - (- 6 . 2) = - 6x + 12
Jadi yang akan dikurangkan adalah - 6x + 12 oleh -2x - 8
= (- 6x + 12) - (-2x - 8)
= - 6x + 12 + 2x + 8
= - 6x + 2x + 12 + 8
= - 4x + 20
So, jawabannya adalah A
Soal 6
Penyederhanan dari
A.
B.
C.
D.
Pembahasan
Bagaimana jika yang dijumlahkan aljabarnya dalam bentuk pecahan??? Tenang saja, ini cukup mudah kok. Kalian hanya perlu mengingat kaidah penjumlahan dan pengurangan pada pecahan biasa.
Pada soal diatas yang menjadi :
a = 5
b = x + 1
c = 6
d = x + 4
Setelah itu, tinggal kita ikuti seperti rumus di atas
=
Yang diatas tinggal kita kalikan angkanya ke dalam suku aljabar, sedangkan yang dibawah kita kalikan menggunakan aturan pengalian suku dua aljabar. Kalian pasti sudah tau caranya.....
=
Kemudian buka kurung yang diatas dan selesaikan oerasinya
=
=
Jadi jawabannya adalah B
Sekian dulu postingan kali ini, semoga dapat mebantu kalian dalam belajar ataupun proses pembelajaran. Jangan lupa di share ya artikel ini.....dan kunjungi juga artikel artikel menarik lainnya. Terimakasih . . . .
